矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
8. 常用矩阵总结——镜面阵，正定阵
8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

8.4 镜面阵

法向量确定一个镜面

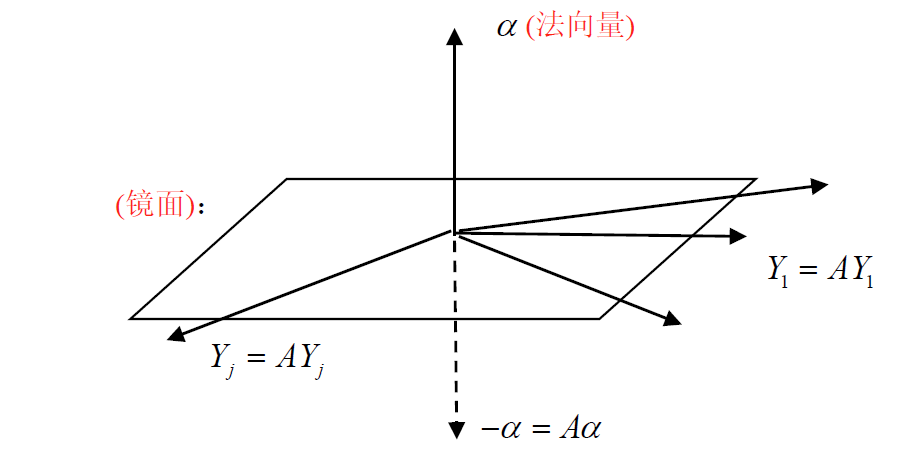
8.4.1 镜面阵的作用

对法向量

• Aα=−αA\alpha=-\alphaAα=−α
• A(Aα)=A2α=αA(A\alpha)=A^2\alpha=\alphaA(Aα)=A2α=α

对镜面上向量

• AY=YAY=YAY=Y

8.4.2 镜面阵表示

A=In−2ααH∣α∣2,其中α=(x1x2⋮xn)∈Cn,且α≠0A=I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2},其中 \alpha=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)\in C^n,且\alpha\neq 0 A=In​−∣α∣22ααH​,其中α=​x1​x2​⋮xn​​​∈Cn,且α=0

令 ϵ=α∣α∣\epsilon=\frac{\alpha}{\vert \alpha\vert}ϵ=∣α∣α​ ，镜面阵 A=I−2ϵϵHA=I-2\epsilon\epsilon^HA=I−2ϵϵH ，满足 ϵHϵ=∣ϵ∣2=1\epsilon^H\epsilon=\vert\epsilon\vert^2=1ϵHϵ=∣ϵ∣2=1

验证：
对于法向量α，Aα=(In−2ααH∣α∣2)α=α−2ααHα∣α∣2=α−2α∣α∣2∣α∣2=−α对于Y∈镜面，有α⊥Y,即内积(α,Y)=(Y,α)=0,且(Y,α)=αHY=0AY=(In−2ααH∣α∣2)Y=Y−2ααHY∣α∣2=Y\begin{aligned} &对于法向量\alpha，A\alpha=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2})\alpha=\alpha-\frac{2\alpha\alpha^H\alpha}{\vert \alpha\vert^2}=\alpha-\frac{2\alpha\vert \alpha\vert^2}{\vert \alpha\vert^2}=-\alpha\\ &对于Y\in 镜面，有\alpha\bot Y,即内积(\alpha,Y)=(Y,\alpha)=0,且(Y,\alpha)=\alpha^HY=0\\ &\quad AY=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2})Y=Y-\frac{2\alpha\alpha^HY}{\vert \alpha\vert^2}=Y \end{aligned} ​对于法向量α，Aα=(In​−∣α∣22ααH​)α=α−∣α∣22ααHα​=α−∣α∣22α∣α∣2​=−α对于Y∈镜面，有α⊥Y,即内积(α,Y)=(Y,α)=0,且(Y,α)=αHY=0AY=(In​−∣α∣22ααH​)Y=Y−∣α∣22ααHY​=Y​

8.4.3 性质

a. 特根

镜面阵至少有两个特征向量 α\alphaα 与 YYY

• Aα=−αA\alpha=-\alphaAα=−α ，特根为 −1-1−1
• AY=YAY=YAY=Y ，特根为 111

代数方法求特根
平移法：A−I=−2ααH∣α∣2为秩1矩阵,特根λ(A−I)={−2∣α∣2tr(ααH),0,⋯,0⏟n−1}==tr(XXH)=XHX=∣X∣2{−2,0,⋯,0}⇒λ(A)=λ(−2ααH∣α∣2)+1={−1,1,⋯,1⏟n−1}\begin{aligned} &平移法：\\ &A-I=-2\frac{\alpha\alpha^H}{\vert \alpha\vert^2}为秩1矩阵,\\ &特根\lambda(A-I)=\{\frac{-2}{\vert \alpha\vert^2}tr(\alpha\alpha^H),\underbrace{0,\cdots,0}_{n-1}\}=\xlongequal{tr(XX^H)=X^HX=\vert X\vert^2}\{-2,0,\cdots,0\}\\ &\Rightarrow \lambda(A)=\lambda\left(-2\frac{\alpha\alpha^H}{\vert \alpha\vert^2}\right)+1=\{-1,\underbrace{1,\cdots,1}_{n-1}\} \end{aligned} ​平移法：A−I=−2∣α∣2ααH​为秩1矩阵,特根λ(A−I)={∣α∣2−2​tr(ααH),n−10,⋯,0​​}=tr(XXH)=XHX=∣X∣2{−2,0,⋯,0}⇒λ(A)=λ(−2∣α∣2ααH​)+1={−1,n−11,⋯,1​​}​
特征多项式 ∣λI−A∣=(λ+1)(λ−1)n−1\vert \lambda I-A\vert=(\lambda+1)(\lambda-1)^{n-1}∣λI−A∣=(λ+1)(λ−1)n−1

b. 特向

镜面上有 n−1n-1n−1 个独立的(线性无关)向量，Y1,Y2,⋯,Yn−1Y_1,Y_2,\cdots,Y_{n-1}Y1​,Y2​,⋯,Yn−1​ (AY1=Y1,AY2=Y2,⋯,AYn−1=Yn−1)(AY_1=Y_1,AY_2=Y_2,\cdots,AY_{n-1}=Y_{n-1})(AY1​=Y1​,AY2​=Y2​,⋯,AYn−1​=Yn−1​) 都是 111 的特向

• Y1,Y2,⋯,Yn−1Y_1,Y_2,\cdots,Y_{n-1}Y1​,Y2​,⋯,Yn−1​ 为 αHX=0\alpha^HX=0αHX=0 的 n−1n-1n−1 个线性无关的解

  证明：
  A−I=−2∣α∣2ααH为秩1矩阵，故α为A−I的特向，r(αH)=1,αHX=0且n−r(αH)=n−1,故αHX=0有n−1个线性无关解Y1,⋯,Yn−1(A−I)X=(−2∣α∣2ααH)X=(−2∣α∣2α)αHX=0⇒Y1,⋯,Yn−1为(A−I)特根为0的根由平移矩阵性质，A−I与A有相同的特根，α,Y1,⋯,Yn−1为A的特征向量(A−I)α=−2α⇒Aα=−α(A−I)Y1=0,⋯,(A−I)Yn−1=0⇒AY1=Y1,⋯,AYn−1=Yn−1\begin{aligned} &A-I=\frac{-2}{\vert \alpha\vert^2}\alpha\alpha^H 为秩1矩阵，故\alpha为A-I的特向，r(\alpha^H)=1,\alpha^HX=0\\ &且n-r(\alpha^H)=n-1,故 \alpha^HX=0有n-1个线性无关解Y_1,\cdots,Y_{n-1}\\ &(A-I)X=(\frac{-2}{\vert \alpha\vert^2}\alpha\alpha^H)X=(\frac{-2}{\vert \alpha\vert^2}\alpha)\alpha^HX=0\Rightarrow Y_1,\cdots,Y_{n-1}为(A-I)特根为0的根\\ &由平移矩阵性质，A-I与A有相同的特根，\alpha,Y_1,\cdots,Y_{n-1}为A的特征向量\\ &(A-I)\alpha=-2\alpha\Rightarrow A\alpha=-\alpha\\ &(A-I)Y_1=0,\cdots,(A-I)Y_{n-1}=0\Rightarrow AY_1=Y_1,\cdots,AY_{n-1}=Y_{n-1} \end{aligned} ​A−I=∣α∣2−2​ααH为秩1矩阵，故α为A−I的特向，r(αH)=1,αHX=0且n−r(αH)=n−1,故αHX=0有n−1个线性无关解Y1​,⋯,Yn−1​(A−I)X=(∣α∣2−2​ααH)X=(∣α∣2−2​α)αHX=0⇒Y1​,⋯,Yn−1​为(A−I)特根为0的根由平移矩阵性质，A−I与A有相同的特根，α,Y1​,⋯,Yn−1​为A的特征向量(A−I)α=−2α⇒Aα=−α(A−I)Y1​=0,⋯,(A−I)Yn−1​=0⇒AY1​=Y1​,⋯,AYn−1​=Yn−1​​

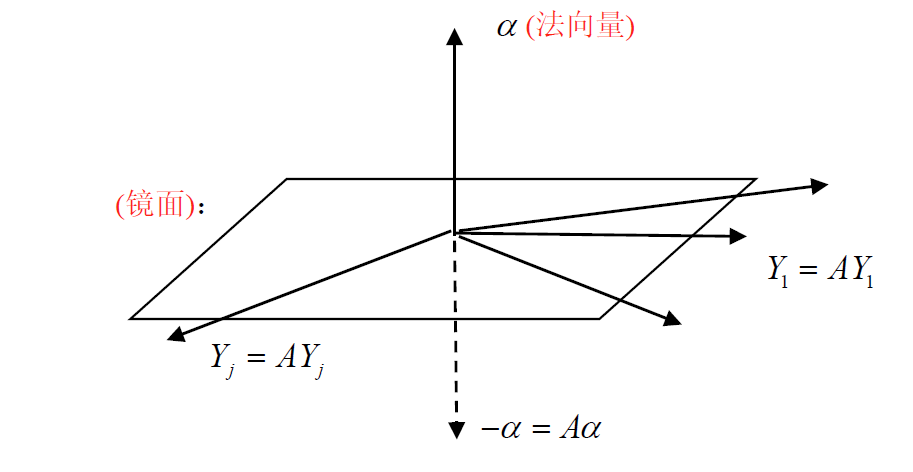
• 镜面阵内 n−1n-1n−1 个特征向量有不同选法，可取 Y1⊥Y2⊥⋯⊥Yn−1Y_1\bot Y_2\bot\cdots\bot Y_{n-1}Y1​⊥Y2​⊥⋯⊥Yn−1​ (互正交)，故可对镜面阵有 nnn 个正交特向 {X⊥Y1⊥Y2⊥⋯⊥Yn−1}\{X\bot Y_1\bot Y_2\bot \cdots \bot Y_{n-1}\}{X⊥Y1​⊥Y2​⊥⋯⊥Yn−1​}

  正规阵，Hermite阵有 nnn 个相互正交的向量

AAA 的全体特根为 λ(A)={−1,1,⋯,1⏟n−1个1}\lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1个1}\}λ(A)={−1,n−1个11,⋯,1​​}

c. 镜面阵为 HermiteHermiteHermite 阵

A=In−2(ααH)∣α∣2A=I_n-\frac{2(\alpha\alpha^H)}{\vert \alpha\vert^2}A=In​−∣α∣22(ααH)​ Hermite阵的差

d. A2=IA^2=IA2=I

A2α=A(Aα)=A(−α)=−(Aα)=−(−α)=αA^2\alpha=A(A\alpha)=A(-\alpha)=-(A\alpha)=-(-\alpha)=\alphaA2α=A(Aα)=A(−α)=−(Aα)=−(−α)=α

即证明： A2=IA^2=IA2=I

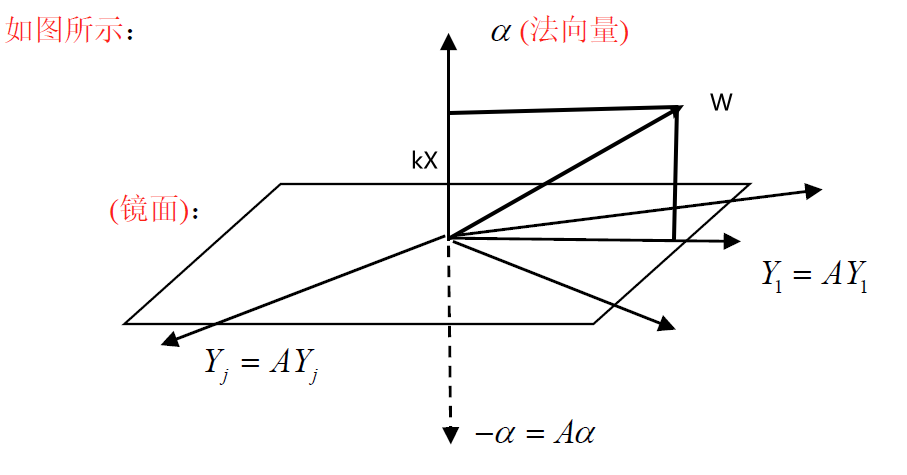
任取Cn中向量W,可分解为W=Y+kα(直角分解)AW=A(Y+kα)=AY+k(Aα)=Y+k(−α)=Y−kα=W~A2W=A(AW)=AW~=A(Y−kα)=AY−kAα=Y+kα=W∀W∈Cn，有A2W=W,故A2=I\begin{aligned} &任取C^n中向量W,可分解为 W=Y+k\alpha(直角分解)\\ &AW=A(Y+k\alpha)=AY+k(A\alpha)=Y+k(-\alpha)=Y-k\alpha=\widetilde{W}\\ &A^2W=A(AW)=A\widetilde{W}=A(Y-k\alpha)=AY-kA\alpha=Y+k\alpha=W\\ &\forall W\in C^n，有A^2W=W,故 A^2=I \end{aligned} ​任取Cn中向量W,可分解为W=Y+kα(直角分解)AW=A(Y+kα)=AY+k(Aα)=Y+k(−α)=Y−kα=WA2W=A(AW)=AW=A(Y−kα)=AY−kAα=Y+kα=W∀W∈Cn，有A2W=W,故A2=I​

A2=(I−2ααH∣α∣2)2=I2−4ααH∣α∣2+4∣α∣4(ααH)2其中(ααH)2=(ααH)(ααH)=α(αHα)αH=∣α∣2ααH⇒A2=I2−4ααH∣α∣2+4∣α∣4(ααH)2=I2−4ααH∣α∣2+4∣α∣4∣α∣2ααH=I\begin{aligned} &A^2=\left(I-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2}\right)^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\left(\alpha\alpha^H\right)^2\\ &其中 (\alpha\alpha^H)^2=(\alpha\alpha^H)(\alpha\alpha^H)=\alpha(\alpha^H\alpha)\alpha^H=\vert \alpha\vert^2\alpha\alpha^H\\ &\Rightarrow A^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\left(\alpha\alpha^H\right)^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\vert \alpha\vert^2\alpha\alpha^H=I \end{aligned} ​A2=(I−∣α∣22ααH​)2=I2−∣α∣24ααH​+∣α∣44​(ααH)2其中(ααH)2=(ααH)(ααH)=α(αHα)αH=∣α∣2ααH⇒A2=I2−∣α∣24ααH​+∣α∣44​(ααH)2=I2−∣α∣24ααH​+∣α∣44​∣α∣2ααH=I​

d. A−1=AA^{-1}=AA−1=A

e. AAA 为优阵

由于 AH=AA^H=AAH=A ，且 A−1=AA^{-1}=AA−1=A ，故 AHA=A−1A=IA^HA=A^{-1}A=IAHA=A−1A=I ，AAA 为优阵

特根 λ(A)={−1,1,⋯,1⏟n−1}\lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1}\}λ(A)={−1,n−11,⋯,1​​} ，特向 α⊥Y1⊥⋯⊥Yn−1\alpha\bot Y_1\bot\cdots\bot Y_{n-1}α⊥Y1​⊥⋯⊥Yn−1​ ，优阵 Q=(α∣α∣,Y1∣Y1∣,⋯,Yn−1∣Yn−1∣)Q=\left(\frac{\alpha}{\vert \alpha\vert},\frac{Y_1}{\vert Y_1\vert},\cdots,\frac{Y_{n-1}}{\vert Y_{n-1}\vert}\right)Q=(∣α∣α​,∣Y1​∣Y1​​,⋯,∣Yn−1​∣Yn−1​​) ，Q−1=QHQ^{-1}=Q^HQ−1=QH

⇒Q−1AQ=QHAQ=D=(−11⋱1)\Rightarrow Q^{-1}AQ=Q^HAQ=D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right)⇒Q−1AQ=QHAQ=D=​−1​1​⋱​1​​ 为对角阵

D=(−11⋱1)D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right)D=​−1​1​⋱​1​​ 为一个特殊镜面阵，法向量指向 xxx 轴方向

8.4.3 向量构造镜面阵

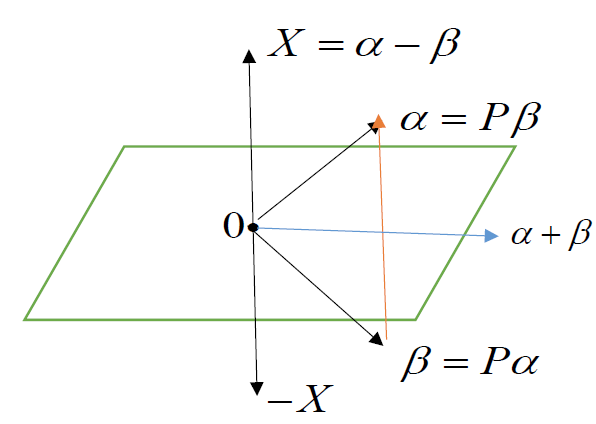
设 RnR^nRn 中2个 实向量，α=(a1⋮an),β=(b1⋮bn)∈Rn\alpha=\left(\begin{matrix}a_1\\\vdots\\a_n\end{matrix}\right),\beta=\left(\begin{matrix}b_1\\\vdots\\b_n\end{matrix}\right)\in R^nα=​a1​⋮an​​​,β=​b1​⋮bn​​​∈Rn ，且 {∣α∣=∣β∣α≠β\left\{ \begin{aligned}&\vert\alpha\vert=\vert\beta\vert\\&\alpha\neq \beta\end{aligned}\right.{​∣α∣=∣β∣α=β​ ，则有镜面阵 P=I−2(α−β)(α−β)H∣(α−β)∣2P=I-\frac{2(\alpha-\beta)(\alpha-\beta)^H}{\vert (\alpha-\beta)\vert^2}P=I−∣(α−β)∣22(α−β)(α−β)H​ ，使得 Pα=β,Pβ=αP\alpha=\beta,P\beta=\alphaPα=β,Pβ=α

证明：
令P=I−2(α−β)(α−β)H∣(α−β)∣2⇒PX=P(α−β)=(α−β)−2(α−β)(α−β)H(α−β)∣(α−β)∣2=−(α−β)=−X(α+β,X)=(α+β,α−β)=(α,α)−(α,β)+(β,α)−(β,β)=∣α∣2−∣β∣2=0⇒法向量(α−β)⊥(α+β),其中(α+β)∈镜面由于{P(α−β)=−(α−β)P(α+β)=(α+β)，两式相加得2Pα=2β⇒Pα=β,P−1β=Pβ=α\begin{aligned} &令P=I-\frac{2(\alpha-\beta)(\alpha-\beta)^H}{\vert (\alpha-\beta)\vert^2}\\ &\Rightarrow PX=P(\alpha-\beta)=(\alpha-\beta)-2\frac{(\alpha-\beta)(\alpha-\beta)^H(\alpha-\beta)}{\vert (\alpha-\beta)\vert^2}=-(\alpha-\beta)=-X\\ &(\alpha+\beta,X)=(\alpha+\beta,\alpha-\beta)=(\alpha,\alpha)-(\alpha,\beta)+(\beta,\alpha)-(\beta,\beta)=\vert \alpha\vert^2-\vert \beta\vert^2=0\\ &\Rightarrow 法向量 (\alpha-\beta)\bot (\alpha+\beta),其中(\alpha+\beta)\in 镜面\\ &由于\left\{ \begin{aligned} &P(\alpha-\beta)=-(\alpha-\beta)\\ &P(\alpha+\beta)=(\alpha+\beta) \end{aligned} \right.，两式相加得2P\alpha=2\beta\Rightarrow P\alpha=\beta,P^{-1}\beta=P\beta=\alpha \end{aligned} ​令P=I−∣(α−β)∣22(α−β)(α−β)H​⇒PX=P(α−β)=(α−β)−2∣(α−β)∣2(α−β)(α−β)H(α−β)​=−(α−β)=−X(α+β,X)=(α+β,α−β)=(α,α)−(α,β)+(β,α)−(β,β)=∣α∣2−∣β∣2=0⇒法向量(α−β)⊥(α+β),其中(α+β)∈镜面由于{​P(α−β)=−(α−β)P(α+β)=(α+β)​，两式相加得2Pα=2β⇒Pα=β,P−1β=Pβ=α​
eg

8.4.4 镜面阵与QR分解

PxP_{x}Px​ 表示 xxx 阶镜面阵 ，AxA_{x}Ax​ 表示 xxx 阶方阵
PnAn=Pn(α1,α2,⋯,αn)=Pnα1=(μ10⋮0)n(μ1∗OAn−1)(100Pn−1)PnAn=(100Pn−1)(μ1∗0An−1)=(μ1∗0Pn−1An−1)=(μ1∗0Pn−1(β1,⋯,βn−1)n−1×n−1)=P2β1=(μ20⋮0)n−1(μ1∗∗0μ2∗00An−2)\begin{aligned} P_nA_n&=P_n(\alpha_1,\alpha_2,\cdots,\alpha_n)\xlongequal{P_n\alpha_1=\left(\begin{matrix}\mu_1\\0\\\vdots\\0\end{matrix}\right)_n}\left( \begin{matrix} \mu_1&*\\ O&A_{n-1} \end{matrix} \right)\\\\ \left( \begin{matrix} 1&0\\0&P_{n-1} \end{matrix} \right)P_nA_n&=\left( \begin{matrix} 1&0\\0&P_{n-1} \end{matrix} \right)\left( \begin{matrix} \mu_1&*\\ 0&A_{n-1} \end{matrix} \right)= \left( \begin{matrix} \mu_1&*\\ 0&P_{n-1}A_{n-1} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*\\ 0&P_{n-1}(\beta_1,\cdots,\beta_{n-1})_{n-1\times n-1 } \end{matrix} \right)\\ &\xlongequal{P_2\beta_1=\left(\begin{matrix}\mu_2\\0\\\vdots\\0\end{matrix}\right)_{n-1}}\left( \begin{matrix} \mu_1&*&*\\ 0&\mu_2&*\\ 0&0&A_{n-2} \end{matrix} \right) \end{aligned} Pn​An​(10​0Pn−1​​)Pn​An​​=Pn​(α1​,α2​,⋯,αn​)Pn​α1​=​μ1​0⋮0​​n​(μ1​O​∗An−1​​)=(10​0Pn−1​​)(μ1​0​∗An−1​​)=(μ1​0​∗Pn−1​An−1​​)=(μ1​0​∗Pn−1​(β1​,⋯,βn−1​)n−1×n−1​​)P2​β1​=​μ2​0⋮0​​n−1​​μ1​00​∗μ2​0​∗∗An−2​​​​

(100⋯0010⋯0001⋯0⋮⋮⋮⋱⋮000⋯P2)⋯(100Pn−1)PnA=(100⋯0010⋯0001⋯0⋮⋮⋮⋱⋮000⋯P2)(μ1∗∗⋯∗0μ2∗⋯∗00μ3⋯∗⋮⋮⋮⋱∗000⋯A2)=(μ1∗∗⋯∗0μ2∗⋯∗00μ3⋯∗⋮⋮⋮⋱∗000⋯P2A2)=(μ1∗∗⋯∗0μ2∗⋯∗00μ3⋯∗⋮⋮⋮⋱∗000⋯P2(γ1,γ2)2×2)=P2γ1=(μn−10)(μ1∗∗⋯∗∗0μ2∗⋯∗∗00μ3⋯∗∗⋮⋮⋮⋱⋮⋮000⋯μn−1⋮000⋯0∗)=R\begin{aligned} \left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right)\cdots\left( \begin{matrix} 1&0\\ 0&P_{n-1} \end{matrix} \right)P_nA&=\left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right) \left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&A_{2} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&P_{2}A_{2} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&P_{2}(\gamma_1,\gamma_2)_{2\times 2} \end{matrix} \right)\\ &\xlongequal{P_2\gamma_1=\left(\begin{matrix}\mu_{n-1}\\0\end{matrix}\right)}\left( \begin{matrix} \mu_1&*&*&\cdots&*&*\\ 0&\mu_2&*&\cdots&*&*\\ 0&0&\mu_3&\cdots&*&*\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&\mu_{n-1}&\vdots\\ 0&0&0&\cdots&0&* \end{matrix} \right)=R\\ \end{aligned} ​100⋮0​010⋮0​001⋮0​⋯⋯⋯⋱⋯​000⋮P2​​​⋯(10​0Pn−1​​)Pn​A​=​100⋮0​010⋮0​001⋮0​⋯⋯⋯⋱⋯​000⋮P2​​​​μ1​00⋮0​∗μ2​0⋮0​∗∗μ3​⋮0​⋯⋯⋯⋱⋯​∗∗∗∗A2​​​=​μ1​00⋮0​∗μ2​0⋮0​∗∗μ3​⋮0​⋯⋯⋯⋱⋯​∗∗∗∗P2​A2​​​=​μ1​00⋮0​∗μ2​0⋮0​∗∗μ3​⋮0​⋯⋯⋯⋱⋯​∗∗∗∗P2​(γ1​,γ2​)2×2​​​P2​γ1​=(μn−1​0​)​μ1​00⋮00​∗μ2​0⋮00​∗∗μ3​⋮00​⋯⋯⋯⋱⋯⋯​∗∗∗⋮μn−1​0​∗∗∗⋮⋮∗​​=R​

故有镜面阵 Q=Pn(100Pn−1)⋯(100⋯0010⋯0001⋯0⋮⋮⋮⋱⋮000⋯P2)Q=P_n\left( \begin{matrix} 1&0\\ 0&P_{n-1} \end{matrix} \right)\cdots\left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right)Q=Pn​(10​0Pn−1​​)⋯​100⋮0​010⋮0​001⋮0​⋯⋯⋯⋱⋯​000⋮P2​​​ ，使 QA=RQA=RQA=R ，由于镜面阵为优H阵 QH=Q−1=QQ^H=Q^{-1}=QQH=Q−1=Q ，故有 QRQRQR 分解 A=QRA=QRA=QR

2阶例题

令α=(1i),∣α∣=2，令β=(20),令镜面法向量X=α−β=(1−2i)XXH=(1−2i)(1−2−i)=((1−2)2−i(1−2)i(1−2)1)=(3−2−i(1−2)i(1−2)1)∣X∣2=XHX=(1−2−i)(1−2i)=2(2−2)镜面阵Q=I2−2XXH∣X∣2=(1001)−22(2−2)(3−22−i(1−2)i(1−2)1)=12(1−ii−1)使得Q(1i)=(20)⇒QA=Q(α1,α2)=(Qα1,Qα2)=(2i20−32)=R解出A的QR分解A=QR,Q=12(1−ii−1)\begin{aligned} &令\alpha=\left( \begin{matrix} 1\\i \end{matrix} \right),\vert\alpha\vert=\sqrt{2}，令 \beta=\left( \begin{matrix} \sqrt{2}\\0 \end{matrix} \right),令镜面法向量X=\alpha-\beta=\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)\\ &XX^H=\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)\left(1-\sqrt{2}\quad -i\right)=\left(\begin{matrix} (1-\sqrt{2})^2&-i(1-\sqrt{2})\\ i(1-\sqrt2)&1 \end{matrix}\right)=\left( \begin{matrix} 3-\sqrt{2}&-i(1-\sqrt{2})\\ i(1-\sqrt{2})&1 \end{matrix} \right)\\ &\vert X\vert^2=X^HX=\left( \begin{matrix} 1-\sqrt{2}\quad -i \end{matrix} \right)\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)=2(2-\sqrt{2})\\ &镜面阵Q=I_2-2\frac{XX^H}{\vert X\vert^2}=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)-\frac{2}{2(2-\sqrt{2})}\left( \begin{matrix} 3-2\sqrt{2}&-i(1-\sqrt{2})\\ i(1-\sqrt{2})&1 \end{matrix} \right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} 1&-i\\i&-1 \end{matrix} \right)\\ &使得 Q\left( \begin{matrix} 1\\i \end{matrix} \right)=\left( \begin{matrix} \sqrt{2}\\0 \end{matrix} \right)\Rightarrow QA=Q(\alpha_1,\alpha_2)=\left(Q\alpha_1,Q\alpha_2\right)=\left( \begin{matrix} \sqrt{2}&\frac{i}{\sqrt{2}}\\ 0&-\frac{3}{\sqrt{2}} \end{matrix} \right)=R\\ &解出A的QR分解 A=QR,Q=\frac{1}{\sqrt{2}}\left( \begin{matrix} 1&-i\\i&-1 \end{matrix} \right) \end{aligned} ​令α=(1i​),∣α∣=2​，令β=(2​0​),令镜面法向量X=α−β=(1−2​i​)XXH=(1−2​i​)(1−2​−i)=((1−2​)2i(1−2​)​−i(1−2​)1​)=(3−2​i(1−2​)​−i(1−2​)1​)∣X∣2=XHX=(1−2​−i​)(1−2​i​)=2(2−2​)镜面阵Q=I2​−2∣X∣2XXH​=(10​01​)−2(2−2​)2​(3−22​i(1−2​)​−i(1−2​)1​)=2​1​(1i​−i−1​)使得Q(1i​)=(2​0​)⇒QA=Q(α1​,α2​)=(Qα1​,Qα2​)=(2​0​2​i​−2​3​​)=R解出A的QR分解A=QR,Q=2​1​(1i​−i−1​)​

3阶例题

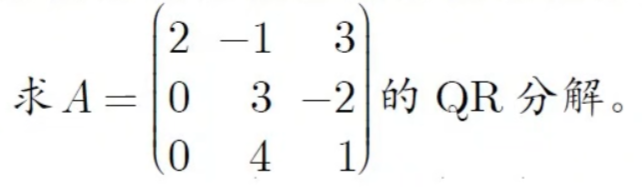
令P3=I,P3(200)=(200),使得P3A=(2∗0A2)令α2=(34),β2=(∣α2∣0)=(50),二维镜面法向量X2=α2−β2=(−24),∣X2∣2=20,XXH=(5−8−816)P2=I2−2∣X2∣2XXH=(354545−35),使得P2A2=(5−250−115)⇒(100P2)P3A=(10003545045−35)A=R=(2−13035−2500−115)故有Q=(100P2)P3=(10003545045−35)，R=(2−13035−2500−115),使得A=QR\begin{aligned} &令P_3=I,P_3\left( \begin{matrix} 2\\0\\0 \end{matrix} \right)=\left( \begin{matrix} 2\\0\\0 \end{matrix} \right),使得P_3A=\left( \begin{matrix} 2&*\\ 0&A_2 \end{matrix} \right)\\ &令\alpha_2=\left( \begin{matrix} 3\\4 \end{matrix} \right),\beta_2=\left( \begin{matrix} \vert \alpha_2\vert\\0 \end{matrix} \right)=\left( \begin{matrix} 5\\0 \end{matrix} \right),二维镜面法向量X_2=\alpha_2-\beta_2=\left( \begin{matrix} -2\\4 \end{matrix} \right),\vert X_2\vert^2=20,XX^H=\left( \begin{matrix} 5&-8\\-8&16 \end{matrix} \right)\\ &\quad P_2=I_2-\frac{2}{\vert X_2\vert^2}XX^H=\left( \begin{matrix} \frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&-\frac{3}{5} \end{matrix} \right),使得P_2A_2=\left( \begin{matrix} 5&-\frac{2}{5}\\0&-\frac{11}{5} \end{matrix} \right)\\ &\Rightarrow\left( \begin{matrix} 1&0\\0&P_2 \end{matrix} \right)P_3A=\left( \begin{matrix} 1&0&0\\ 0&\frac{3}{5}&\frac{4}{5}\\ 0&\frac{4}{5}&-\frac{3}{5} \end{matrix} \right)A=R=\left( \begin{matrix} 2&-1&3\\ 0&\frac{3}{5}&-\frac{2}{5}\\ 0&0&-\frac{11}{5} \end{matrix} \right)\\ &故有Q=\left( \begin{matrix} 1&0\\ 0&P_2 \end{matrix} \right)P_3=\left( \begin{matrix} 1&0&0\\ 0&\frac{3}{5}&\frac{4}{5}\\ 0&\frac{4}{5}&-\frac{3}{5} \end{matrix} \right)，R=\left( \begin{matrix} 2&-1&3\\ 0&\frac{3}{5}&-\frac{2}{5}\\ 0&0&-\frac{11}{5} \end{matrix} \right),使得A=QR \end{aligned} ​令P3​=I,P3​​200​​=​200​​,使得P3​A=(20​∗A2​​)令α2​=(34​),β2​=(∣α2​∣0​)=(50​),二维镜面法向量X2​=α2​−β2​=(−24​),∣X2​∣2=20,XXH=(5−8​−816​)P2​=I2​−∣X2​∣22​XXH=(53​54​​54​−53​​),使得P2​A2​=(50​−52​−511​​)⇒(10​0P2​​)P3​A=​100​053​54​​054​−53​​​A=R=​200​−153​0​3−52​−511​​​故有Q=(10​0P2​​)P3​=​100​053​54​​054​−53​​​，R=​200​−153​0​3−52​−511​​​,使得A=QR​

8.5 正定阵

8.5.1 二次型

a. 二次型定义

令 AAA 为 HermiteHermiteHermite 阵 (AH=A∈Cn×n)(A^H=A\in C^{n\times n})(AH=A∈Cn×n)， X=(x1x2⋮xn)X=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right)X=​x1​x2​⋮xn​​​ ，称 XHAX=(x1‾,x2‾,⋯,xn‾)A(x1x2⋮xn)X^HAX=\left(\overline{x_1},\overline{x_2},\cdots,\overline{x_n}\right)A\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right)XHAX=(x1​​,x2​​,⋯,xn​​)A​x1​x2​⋮xn​​​ ，为矩阵 AAA 产生的二次型，记为 f(x)=XHAXf(x)=X^HAXf(x)=XHAX

b. 正定二次型与正定阵定义

若 AH=AA^H=AAH=A ,对一切 X≠0X\neq 0X=0 ,有 XHAX>0X^HAX>0XHAX>0 ,则 f(x)=XHAXf(x)=X^HAXf(x)=XHAX 为正定二次型，A为正定阵，记为 A>0A>0A>0
若 AH=AA^H=AAH=A ,对一切 X≠0X\neq 0X=0 ，有 XHAX≥0X^HAX\ge 0XHAX≥0 ,则 f(x)=XHAXf(x)=X^HAXf(x)=XHAX 为半正定二次型，A为半正定阵，记为 A≥0A\ge 0A≥0

8.5.2 正定阵的定理

A>0⟺A>0\iffA>0⟺ AAA 为Hermite阵，且 λ1,λ2,⋯,λn>0\lambda_1,\lambda_2,\cdots,\lambda_n > 0λ1​,λ2​,⋯,λn​>0
A≥0⟺A\ge 0 \iffA≥0⟺ AAA 为Hermite阵，且 λ1,λ2,⋯,λn≥0\lambda_1,\lambda_2,\cdots,\lambda_n \ge 0λ1​,λ2​,⋯,λn​≥0

证明

⇒\Rightarrow⇒

若 AAA 为正定阵，则 AAA 生成的二次型 f(x)=XHAX>0f(x)=X^HAX>0f(x)=XHAX>0 ，∴λi=XHAX∣X∣2>0\therefore \lambda_i=\frac{X^HAX}{\vert X\vert^2}>0∴λi​=∣X∣2XHAX​>0

⇐\Leftarrow⇐
由Hermite分解定理，A为Hermite阵，则存在U阵Q，使得QHAQ=Λ=(λ1⋱λn)∴A=ΔΛ,而λi>0，Λ为正定阵，故A为正定阵\begin{aligned} &由Hermite分解定理，A为Hermite阵，则存在U阵Q，\\ &使得Q^HAQ=\Lambda=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\quad\\ &\quad&\lambda_n\\ \end{matrix} \right)\\ &\therefore A\overset{\Delta}{=}\Lambda,而\lambda_i>0，\Lambda 为正定阵，故A为正定阵 \end{aligned} ​由Hermite分解定理，A为Hermite阵，则存在U阵Q，使得QHAQ=Λ=​λ1​​⋱​λn​​​∴A=ΔΛ,而λi​>0，Λ为正定阵，故A为正定阵​
单位阵是正定阵 ：λi=1\lambda_i= 1λi​=1 显然大于0

8.5.3 正定阵间必合同

1. A>0（正定阵）⟺A=ΔΛA>0（正定阵） \iff A\overset{\Delta}{=}\LambdaA>0（正定阵）⟺A=ΔΛ
2. Λ=ΔI\Lambda\overset{\Delta}{=}IΛ=ΔI 对角阵一定合同于单位阵
3. 若A,B为同阶正定阵，则 A=ΔBA\overset{\Delta}{=} BA=ΔB

证明1：
若A正定，则有AH=A由Hermite分解定理，必∃优阵Q使得QHAQ=Λ,且λi>0\begin{aligned} &若A正定，则有A^H=A\\ &由Hermite分解定理，必\exist 优阵Q使得Q^HAQ=\Lambda,且\lambda_i>0\\ \end{aligned} ​若A正定，则有AH=A由Hermite分解定理，必∃优阵Q使得QHAQ=Λ,且λi​>0​
证明2：
若Λ=(λ1⋱λn),其中λi>0⇒f(x)=XHΛX=λ1∣x1∣2+λ2∣x2∣2+⋯+λn∣xn∣2>0⇒可分解为Λ=(λ1⋱λn)I(λ1⋱λn)=PIP可知P可逆，且PH=P,故PHIP=Λ即对角正定阵合同于单位阵，记为Λ=ΔI\begin{aligned} 若\Lambda&=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\\ &&\lambda_n \end{matrix} \right),其中\lambda_i>0\\ &\Rightarrow f(x)=X^H\Lambda X=\lambda_1\vert x_1\vert^2+\lambda_2\vert x_2\vert^2+\cdots+\lambda_n\vert x_n\vert^2>0\\ &\Rightarrow 可分解为\Lambda=\left( \begin{matrix} \sqrt{\lambda_1}&\quad&\quad\\ \quad&\ddots&\quad\\ \quad&\quad&\sqrt{\lambda_n}\\ \end{matrix} \right)I\left( \begin{matrix} \sqrt{\lambda_1}&&\\ &\ddots&\\ &&\sqrt{\lambda_n}\\ \end{matrix} \right)\\ &\quad \quad\quad\quad\quad \quad \quad=PIP\\ &可知P可逆，且P^H=P,故P^HIP=\Lambda\\ &即对角正定阵合同于单位阵，记为\Lambda\overset{\Delta}{=}I \end{aligned} 若Λ​=​λ1​​⋱​λn​​​,其中λi​>0⇒f(x)=XHΛX=λ1​∣x1​∣2+λ2​∣x2​∣2+⋯+λn​∣xn​∣2>0⇒可分解为Λ=​λ1​​​⋱​λn​​​​I​λ1​​​⋱​λn​​​​=PIP可知P可逆，且PH=P,故PHIP=Λ即对角正定阵合同于单位阵，记为Λ=ΔI​
证明3：
由A>0,B>0,则A=ΔI,B=ΔI⇒A=ΔB\begin{aligned} &由A>0,B>0,则A\overset{\Delta}{=}I,B\overset{\Delta}{=}I\Rightarrow A\overset{\Delta}{=}B \end{aligned} ​由A>0,B>0,则A=ΔI,B=ΔI⇒A=ΔB​

8.5.4 乘积形式的正定阵

1. 对一切矩阵 A=An×pA=A_{n\times p}A=An×p​ 且 n≥pn\ge pn≥p ，AHAA^HAAHA 与 AAHAA^HAAH 都是Hermite阵
2. AHAA^HAAHA 与 AAHAA^HAAH 只相差 n−pn-pn−p 个0根
3. AHA≥0A^HA\ge0AHA≥0 ，AHA≥0A^HA\ge 0AHA≥0
4. r(AHA)=r(AAH)=r(A)r(A^HA)=r(AA^H)=r(A)r(AHA)=r(AAH)=r(A)

a. AHAA^HAAHA 为Hermite阵

(AHA)H=AHA，且(AAH)H=AAH，则AHA与AAH为Hermite阵\begin{aligned} (A^HA)^H=A^HA，且(AA^H)^H=AA^H，则A^HA与AA^H为Hermite阵 \end{aligned} (AHA)H=AHA，且(AAH)H=AAH，则AHA与AAH为Hermite阵​

b. AHA与AAHA^HA与AA^HAHA与AAH 相差n-p个0根

A=An×p,B=p×n,且n≥p由换位公式∣λI−AB∣=λn−p∣λI−BA∣,则AB与BA必有相同的非零根，故AHA与AAH只相差n−p个零根\begin{aligned} &A=A_{n\times p},B={p\times n},且n\ge p\\ &由换位公式 \vert \lambda I-AB\vert=\lambda^{n-p}\vert \lambda I-BA \vert,\\ &则 AB与BA必有相同的非零根，故A^HA与AA^H只相差n-p个零根 \end{aligned} ​A=An×p​,B=p×n,且n≥p由换位公式∣λI−AB∣=λn−p∣λI−BA∣,则AB与BA必有相同的非零根，故AHA与AAH只相差n−p个零根​

c. AHA与AAHA^HA与AA^HAHA与AAH 是半正定阵（不是方阵的正定阵）

对任意非零向量X，有二次型f(x)=XHAHAX=(AX)H(AX)=∣AX∣2≥0,可知f(x)为半正定二次型，AHA为半正定阵\begin{aligned} &对任意非零向量X，有二次型f(x)=X^HA^HAX=(AX)^H(AX)=\vert AX \vert^2\ge 0,\\ &可知f(x)为半正定二次型，A^HA为半正定阵 \end{aligned} ​对任意非零向量X，有二次型f(x)=XHAHAX=(AX)H(AX)=∣AX∣2≥0,可知f(x)为半正定二次型，AHA为半正定阵​

d. r(AAH)=r(AHA)=r(A)r(AA^H)=r(A^HA)=r(A)r(AAH)=r(AHA)=r(A)

由AHA为半正定阵，则AHA与AAH都只有非负根可写为λ(AHA)={λ1,λ2,...λp}≥0由换位公式，知λAHA与λAAH只相差n−p个零根∴λ(AAH)={λ1,λ2,...,λp,0,0,...,0}≥0r(AHA)=r(AAH)=p=r(A)=r(AH)\begin{aligned} &由A^HA为半正定阵，则A^HA与AA^H都只有非负根\\ &可写为\lambda(A^HA)=\{\lambda_1,\lambda_2,...\lambda_p\}\ge 0\\ &由换位公式，知\lambda{A^HA}与\lambda{AA^H}只相差n-p个零根\\ &\therefore \lambda(AA^H)=\{\lambda_1,\lambda_2,...,\lambda_p,0,0,...,0\}\ge 0\\ &r(A^HA)=r(AA^H)=p=r(A)=r(A^H) \end{aligned} ​由AHA为半正定阵，则AHA与AAH都只有非负根可写为λ(AHA)={λ1​,λ2​,...λp​}≥0由换位公式，知λAHA与λAAH只相差n−p个零根∴λ(AAH)={λ1​,λ2​,...,λp​,0,0,...,0}≥0r(AHA)=r(AAH)=p=r(A)=r(AH)​

齐次方程组AX=0,AHAX=0，解集相同(同解)若(AHA)X=0成立，则∣AX∣2=(AX)H(AX)=XHAHAX=(AX)2=0∴AX=0,r(AHA)=r(A)\begin{aligned} &齐次方程组AX=0,A^HAX=0，解集相同(同解)\\ &若(A^HA)X=0成立，则\vert AX \vert^2=(AX)^H(AX)=X^HA^HAX=(AX)^2=0\\ &\therefore AX=0,r(A^HA)=r(A) \end{aligned} ​齐次方程组AX=0,AHAX=0，解集相同(同解)若(AHA)X=0成立，则∣AX∣2=(AX)H(AX)=XHAHAX=(AX)2=0∴AX=0,r(AHA)=r(A)​